Image Derivatives

This paper propose an efficient way to combine different spline types for computing first and second order derivatives (please see my video presentation). The following formula is derived, which shows that a spline surface can be rewritten as an outer product and a convolution

Note that this equation is differentiable and this fact is used to create filter kernels for computing smooth derivatives.

• Simple filter design for first and second order derivatives by a double filtering approach.  A. Hast. Pattern Recognition Letters, Vol. 42, no.1 June, pp. 65-71. 2014.

  @article{DBLP:journals/prl/Hast14, 
  author = {Anders Hast},
  title = {Simple filter design for first and second order derivatives by a double filtering approach}, 
  journal = {Pattern Recognition Letters}, 
  volume = {42}, 
  pages = {65--71}, 
  year = {2014}, 
  url = {https://doi.org/10.1016/j.patrec.2014.01.014}, 
  doi = {10.1016/j.patrec.2014.01.014}}

The first derivatives are

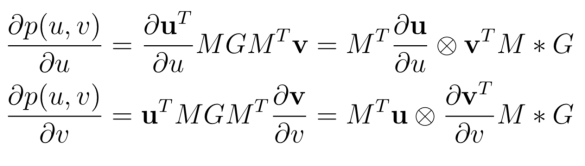
And the second derivatives are

The paper also discuss the use of Trigonometric splines and they appear to have some advantages over cubic splines

The code is available on the code page!